24+ Solution Set Of Inequalities Examples

Solution Set Of Inequalities Examples. X + 3 <= 10. 2 x + 1 > 9and3 x + 4 < 10 solution solving the inequalities separately, we get 2 x > 8 3 x < 6 and x > 4 x < 2.

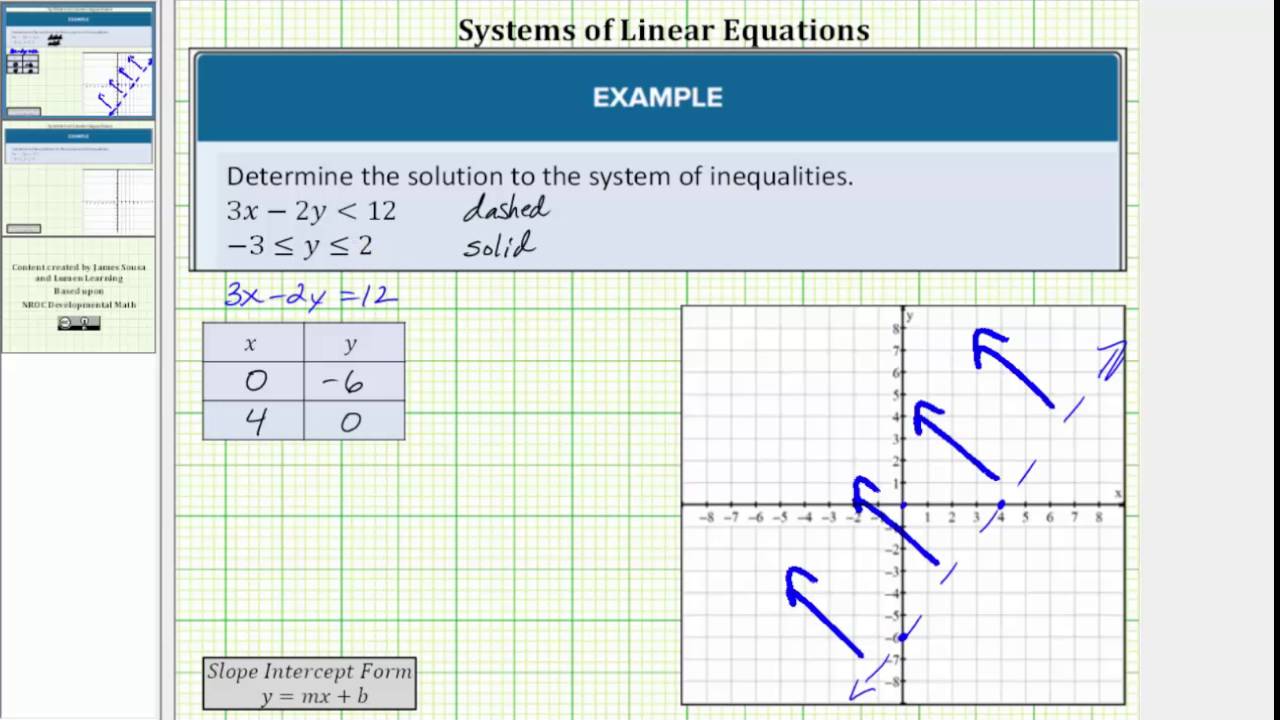
Because of the strict inequalities, we will use a dashed line for each boundary. Example the solution to the inequality. Example 2x+ 1 3 is an inequality.

ryanair airports europe seven hours pic hd salle de bain beton cire scie sabre stanley fme365k

Introduction to Inequalities and Interval Notation

The solution to this compound inequality is all the values of x in which x is either greater than 6 or x is less than 2. For example, x > 6 or x < 2. X + 3 <= 10. These ideas and techniques extend to nonlinear inequalities with two variables.

Do you see how the inequality sign still points at the smaller value (7) ? This set may have in nitely many numbers and may be represented by an interval or a number of intervals on the real line. Because of the strict inequalities, we will use a dashed line for each boundary. This is also called the feasible set.

3 2.5 2 1.5 1 0.5 ð 0.5 ð 1 ð 1. Compound inequalities with no solution. For example, x > 6 or x < 2. Solving and graphing compound inequalities in the form of “or”. If we subtract 5 from both sides, we get:

An absolute value inequality is slightly different to an absolute value equation, examples of which can be seen on the absolute value equations page. For the first inequality shade all points above the boundary and for the second inequality shade all points below the boundary. 2x + 3 ≤ 7. ∅ 1.3.1quadratic inequalities a quadratic inequality (in one unknown) is..

The solutions were exact numbers. The “or” word can give us a larger solution set, while “and” can give us a smaller solution set. The solution of an inequality is the set of all numbers which satisfy the inequality. Let's take a closer look at a compound inequality that uses or to combine two inequalities. If we subtract 5 from.

Z = −5 z = − 5 in 2(z−5) ≤ 4z 2 ( z − 5) ≤ 4 z. An absolute value inequality is slightly different to an absolute value equation, examples of which can be seen on the absolute value equations page. For the first inequality shade all points above the boundary and for the second inequality shade all.

For instance, x > 2 or x < 3. Remember that a compound inequality contains linking words such as “or” & “and”. ∈ x > 4 and x < 2} =. Do you see how the inequality sign still points at the smaller value (7) ? So let us flip sides (and the inequality sign!):

Let’s take a closer look at a compound inequality that uses or to combine two inequalities. Graph the following system of linear inequalities: Dividing both sides by 2, x ≤ 2 We begin by solving both inequalities for y. Z = −5 z = − 5 in 2(z−5) ≤ 4z 2 ( z − 5) ≤ 4 z.